Search results for Erosion

Upper Antelope Canyon, a deep, narrow and spectacular slot canyon lying on Navajo Tribal lands near Page, Arizona.
Location: Navajo Tribal Lands, Page, Arizona
Image ID: 35932  

Upper Antelope Canyon, a deep, narrow and spectacular slot canyon lying on Navajo Tribal lands near Page, Arizona.
Location: Navajo Tribal Lands, Page, Arizona
Image ID: 35933  

Spectacular Horseshoe Bend sunrise. The Colorado River makes a 180-degree turn at Horseshoe Bend. Here the river has eroded the Navajo sandstone for eons, digging a canyon 1100-feet deep.
Location: Horseshoe Bend, Page, Arizona
Image ID: 35941  

Canyon X, a spectacular slot canyon near Page, Arizona. Slot canyons are formed when water and wind erode a cut through a (usually sandstone) mesa, producing a very narrow passage that may be as slim as a few feet and a hundred feet or more in height.
Location: Page, Arizona
Image ID: 36013  

Owl Canyon, a beautiful slot canyon that is part of the larger Antelope Canyon system. Page, Arizona.
Location: Navajo Tribal Lands, Page, Arizona
Image ID: 36028  

Rattlesnake Canyon, a beautiful slot canyon that is part of the larger Antelope Canyon system. Page, Arizona.
Location: Navajo Tribal Lands, Page, Arizona
Image ID: 36034  

Rattlesnake Canyon, a beautiful slot canyon that is part of the larger Antelope Canyon system. Page, Arizona.
Location: Navajo Tribal Lands, Page, Arizona
Image ID: 36038  

Lower Antelope Canyon, a deep, narrow and spectacular slot canyon lying on Navajo Tribal lands near Page, Arizona.
Location: Navajo Tribal Lands, Page, Arizona
Image ID: 37767  

Lower Antelope Canyon, a deep, narrow and spectacular slot canyon lying on Navajo Tribal lands near Page, Arizona.
Location: Navajo Tribal Lands, Page, Arizona
Image ID: 37768  

Lower Antelope Canyon, a deep, narrow and spectacular slot canyon lying on Navajo Tribal lands near Page, Arizona.
Location: Navajo Tribal Lands, Page, Arizona
Image ID: 37773  

Pedestal rock, or hoodoo, at Stud Horse Point. These hoodoos form when erosion occurs around but not underneath a more resistant caprock that sits atop of the hoodoo spire. Stud Horse Point is a spectacular viewpoint on a mesa overlooking the Arizona / Utah border.
Location: Page, Arizona
Image ID: 37778  

Pedestal rock, or hoodoo, at Stud Horse Point. These hoodoos form when erosion occurs around but not underneath a more resistant caprock that sits atop of the hoodoo spire. Stud Horse Point is a spectacular viewpoint on a mesa overlooking the Arizona / Utah border.
Location: Page, Arizona
Image ID: 37780  

Sunrise light touches the Fins. Sandstone fins stand on edge. Vertical fractures separate standing plates of sandstone that are eroded into freestanding fins, that may one day further erode into arches.
Location: Arches National Park, Utah
Image ID: 29255  

Aerial view of the lagoon inside Clipperton Island. The lagoon within the atoll was formerly open to the ocean but has been closed and stagnant for many decades. Some experts believe erosion will open the lagoon up to the ocean again soon. Clipperton Island, a minor territory of France also known as Ile de la Passion, is a spectacular coral atoll in the eastern Pacific. By permit HC / 1485 / CAB (France).
Location: Clipperton Island, France
Image ID: 32866  

Natural arch formed in sandstone frames the setting moon.
Location: Valley of Fire State Park, Nevada
Image ID: 26486  

The Fire Wave, a beautiful sandstone formation exhibiting dramatic striations, striped layers in the geologic historical record.
Location: Valley of Fire State Park, Nevada
Image ID: 26487  

Broken Hill with the Pacific Ocean in the distance. Broken Hill is an ancient, compacted sand dune that was uplifted to its present location and is now eroding.
Location: Torrey Pines State Reserve, San Diego, California
Image ID: 14758  

The Wave, an area of fantastic eroded sandstone featuring beautiful swirls, wild colors, countless striations, and bizarre shapes set amidst the dramatic surrounding North Coyote Buttes of Arizona and Utah. The sandstone formations of the North Coyote Buttes, including the Wave, date from the Jurassic period. Managed by the Bureau of Land Management, the Wave is located in the Paria Canyon-Vermilion Cliffs Wilderness and is accessible on foot by permit only.
Location: North Coyote Buttes, Paria Canyon-Vermilion Cliffs Wilderness, Arizona
Image ID: 20609  

Sunrise lights sandstone rocks, Valley of Fire.
Location: Valley of Fire State Park, Nevada
Image ID: 28444  

Sunrise lights sandstone rocks, Valley of Fire.
Location: Valley of Fire State Park, Nevada
Image ID: 28445  

Sunrise lights sandstone rocks, Valley of Fire.
Location: Valley of Fire State Park, Nevada
Image ID: 28446  

The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10368  

The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10369  

Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10375  

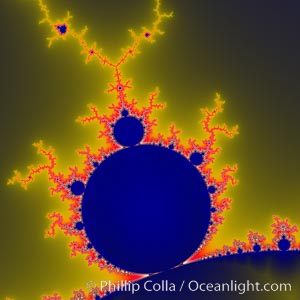
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10378  

Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10383  

Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10391  

Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10395  

The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 18729  

The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 18731