Search results for Square

-1- 2 3 4 5
San Diego Convention Center Skyline and Waterfront at Sunrise. San Diego Convention Center, located in the Marina District of downtown San Diego. Built in 1989, the San Diego Convention Center offers 525,700 square feet of exhibit space. It is noted for its distinctive "sails" made of Teflon-coated fiberglass suspended over the central exhibition hall, aptly named Sails Pavilion
San Diego Convention Center Skyline and Waterfront at Sunrise. San Diego Convention Center, located in the Marina District of downtown San Diego. Built in 1989, the San Diego Convention Center offers 525,700 square feet of exhibit space. It is noted for its distinctive "sails" made of Teflon-coated fiberglass suspended over the central exhibition hall, aptly named Sails Pavilion.
Location: San Diego, California
Image ID: 40046  
Panorama dimensions: 5186 x 13999
San Diego Convention Center, located in the Marina District of downtown San Diego. Built in 1989, the San Diego Convention Center offers 525,700 square feet of exhibit space. It is noted for its distinctive "sails" made of Teflon-coated fiberglass suspended over the central exhibition hall, aptly named Sails Pavilion
San Diego Convention Center, located in the Marina District of downtown San Diego. Built in 1989, the San Diego Convention Center offers 525,700 square feet of exhibit space. It is noted for its distinctive "sails" made of Teflon-coated fiberglass suspended over the central exhibition hall, aptly named Sails Pavilion.
Location: San Diego, California
Image ID: 22290  
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10368  
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10369  
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10375  
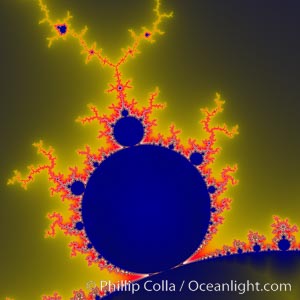
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10378  
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10383  
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10391  
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
Detail within the Mandelbrot set fractal. This detail is found by zooming in on the overall Mandelbrot set image, finding edges and buds with interesting features. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 10395  
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 18729  
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 18731  
Fractal design. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
Fractal design. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 18732  
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 18737  
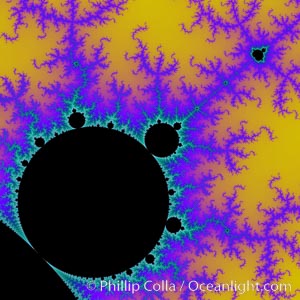
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set, Mandelbrot set
The Mandelbrot Fractal. Fractals are complex geometric shapes that exhibit repeating patterns typified by self-similarity, or the tendency for the details of a shape to appear similar to the shape itself. Often these shapes resemble patterns occurring naturally in the physical world, such as spiraling leaves, seemingly random coastlines, erosion and liquid waves. Fractals are generated through surprisingly simple underlying mathematical expressions, producing subtle and surprising patterns. The basic iterative expression for the Mandelbrot set is z = z-squared + c, operating in the complex (real, imaginary) number set.
Species: Mandelbrot fractal, Mandelbrot set
Image ID: 18739  
Truncate Butterflyfish, Chelmonops curiosus, Kangaroo Island, South Australia, Chelmonops curiosus
Truncate Butterflyfish, Chelmonops curiosus, Kangaroo Island, South Australia.
Species: Truncate Butterflyfish, Chelmonops curiosus
Location: Kangaroo Island, South Australia
Image ID: 39221  
July Column in the Place de la Bastille. The Place de la Bastille is a square in Paris, where the Bastille prison stood until the 'Storming of the Bastille' and its subsequent physical destruction between 14 July 1789 and 14 July 1790 during the French Revolution. The square straddles 3 arrondissements of Paris, namely the 4th, 11th and 12th. The July Column (Colonne de Juillet) which commemorates the events of the July Revolution (1830) stands at the center of the square
July Column in the Place de la Bastille. The Place de la Bastille is a square in Paris, where the Bastille prison stood until the 'Storming of the Bastille' and its subsequent physical destruction between 14 July 1789 and 14 July 1790 during the French Revolution. The square straddles 3 arrondissements of Paris, namely the 4th, 11th and 12th. The July Column (Colonne de Juillet) which commemorates the events of the July Revolution (1830) stands at the center of the square.
Location: Place de la Bastille, Paris, France
Image ID: 28248  
Point Loma Wastewater Treatment Plant and Fort Rosecrans, Point Loma. Opened in 1963, the Point Loma Wastewater Treatment Plant treats approximately 175 million gallons of wastewater per day, generated by 2.2 million residents of San Diego over a 450 square mile area. San Diego Bay, Coronado Island and downtown San Diego are seen in the distance
Point Loma Wastewater Treatment Plant and Fort Rosecrans, Point Loma. Opened in 1963, the Point Loma Wastewater Treatment Plant treats approximately 175 million gallons of wastewater per day, generated by 2.2 million residents of San Diego over a 450 square mile area. San Diego Bay, Coronado Island and downtown San Diego are seen in the distance.
Image ID: 30758  
July Column in the Place de la Bastille. The Place de la Bastille is a square in Paris, where the Bastille prison stood until the 'Storming of the Bastille' and its subsequent physical destruction between 14 July 1789 and 14 July 1790 during the French Revolution. The square straddles 3 arrondissements of Paris, namely the 4th, 11th and 12th. The July Column (Colonne de Juillet) which commemorates the events of the July Revolution (1830) stands at the center of the square
July Column in the Place de la Bastille. The Place de la Bastille is a square in Paris, where the Bastille prison stood until the 'Storming of the Bastille' and its subsequent physical destruction between 14 July 1789 and 14 July 1790 during the French Revolution. The square straddles 3 arrondissements of Paris, namely the 4th, 11th and 12th. The July Column (Colonne de Juillet) which commemorates the events of the July Revolution (1830) stands at the center of the square.
Location: Place de la Bastille, Paris, France
Image ID: 28249  
Neon lights fill Times Square at night, New York City
Neon lights fill Times Square at night.
Location: Times Square, New York City
Image ID: 11199  
Badwater, California. Badwater, at 282 feet below sea level, is the lowest point in North America. 9000 square miles of watershed drain into the Badwater basin, to dry and form huge white salt flats, Death Valley National Park
Badwater, California. Badwater, at 282 feet below sea level, is the lowest point in North America. 9000 square miles of watershed drain into the Badwater basin, to dry and form huge white salt flats.
Location: Badwater, Death Valley National Park, California
Image ID: 15579  
Badwater, California. Badwater, at 282 feet below sea level, is the lowest point in North America. 9000 square miles of watershed drain into the Badwater basin, to dry and form huge white salt flats, Death Valley National Park
Badwater, California. Badwater, at 282 feet below sea level, is the lowest point in North America. 9000 square miles of watershed drain into the Badwater basin, to dry and form huge white salt flats.
Location: Badwater, Death Valley National Park, California
Image ID: 15580  
Point Loma Wastewater Treatment Plant. Opened in 1963, the Point Loma Wastewater Treatment Plant treats approximately 175 million gallons of wastewater per day, generated by 2.2 million residents of San Diego over a 450 square mile area. San Diego Bay, Coronado Island and downtown San Diego are seen in the distance
Point Loma Wastewater Treatment Plant. Opened in 1963, the Point Loma Wastewater Treatment Plant treats approximately 175 million gallons of wastewater per day, generated by 2.2 million residents of San Diego over a 450 square mile area. San Diego Bay, Coronado Island and downtown San Diego are seen in the distance.
Location: San Diego, California
Image ID: 22315  
San Diego Convention Center, located in the Marina District of downtown San Diego. Built in 1989, the San Diego Convention Center offers 525,700 square feet of exhibit space. It is noted for its distinctive "sails" made of Teflon-coated fiberglass suspended over the central exhibition hall, aptly named Sails Pavilion
San Diego Convention Center, located in the Marina District of downtown San Diego. Built in 1989, the San Diego Convention Center offers 525,700 square feet of exhibit space. It is noted for its distinctive "sails" made of Teflon-coated fiberglass suspended over the central exhibition hall, aptly named Sails Pavilion.
Location: San Diego, California
Image ID: 22369  
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture.
Location: Phoenix Convention Center, Arizona
Image ID: 23175  
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture.
Location: Phoenix Convention Center, Arizona
Image ID: 23179  
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture.
Location: Phoenix Convention Center, Arizona
Image ID: 23184  
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture.
Location: Phoenix Convention Center, Arizona
Image ID: 23189  
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture.
Location: Phoenix Convention Center, Arizona
Image ID: 23192  
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture.
Location: Phoenix Convention Center, Arizona
Image ID: 23196  
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture
Phoenix Convention Center. Originally built in 1972 and expanded in 1985 and the mid-90's, the Phoenix Convention center offers 300,000 square feet of space for conventions year round. It's exterior is a mix of modern glass, metal and stone architecture.
Location: Phoenix Convention Center, Arizona
Image ID: 23197  
-1- 2 3 4 5
Permalink: Square photos

All photographs copyright © Phillip Colla / Oceanlight.com, all rights reserved worldwide.